3D spheres without 3D

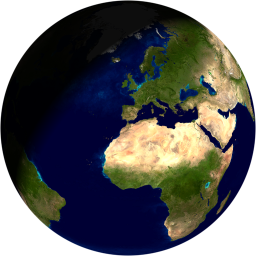
Most spheres in games and programs are texture-mapped tessellated polygonal spheres. This is because they're simple to model and render. Properly subdivided geospheres look good and hardware tessellation can even make the polygonal edges go away. However, it is possible to draw perfectly smooth and round spheres in 2D and using only 3D math in certain parts.

Spheres can be rendered easily by just looping over the area, and checking if the point is inside the sphere's radius. Then, for every pixel that is inside, use trigonometry to figure out the texture coordinate. Shading can be done if you compute the dot product between light and surface normal on that point. Simple and fast.

Sphere rendering is simple:

1. Determine visible area (with radius and clipping boxes)
2. Compute light position in 3D space
3. Iterate over the visible sphere area and for each pixel inside the sphere, do this:
   1. Determine the Z coordinate from X and Y coordinates (Pythagoras' theorem)
   2. Rotate the 3D point with the rotation matrix
   3. Compute light intensity (dot product between the surface normal and light)
   4. Use spherical mapping to determine texture coordinates
   5. Get texel, shade and output it

Because of the simplicity, this can be done somewhat quickly even in software. A pixel shader version is very straightforward to code and it looks vastly better due to texture filtering and other goodies. The software version can be multithreaded somewhat easily, because the sphere can be split into equal areas that do not overlap.

The texture map used in the above image was taken from here.

GLSL implementation

The shader files are in the source ZIP below. The GLSL version requires you to just draw one square polygon with proper texture coordinates. The texture coordinates are from -1 to 1, so we can use them directly to determine which pixels are inside the sphere (with a radius of 1):

A live WebGL demo of this is available here. It uses slightly modified shaders (modifications required by WebGL).

const float w = 512.0f,
            h = 512.0f;

const float vertices[4] =
{
    // X     Y      S      T
    { 0.0f,    h, -1.0f,  1.0f },
    {    w,    h,  1.0f,  1.0f },
    {    w, 0.0f,  1.0f, -1.0f },
    { 0.0f, 0.0f, -1.0f, -1.0f },
};

...

glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

...

glBindBuffer(GL_ARRAY_BUFFER, vbo);

glUseProgram(sphere);
GLint pos = glGetAttribLocation(sphere, "vertex");

glEnableVertexAttribArray(pos);
glVertexAttribPointer(pos, 4, GL_FLOAT, GL_FALSE, sizeof(float) * 4, (GLvoid *)0);

// shader parameters omitted here
glDrawArrays(GL_TRIANGLE_FAN, 0, 4);

// cleanup omitted

Parameters

The following parameters control the shader:

• tex: The texture map for the sphere.
• color: Used to colorize the final output (essentially emulates glColor3f). Usually set to (1.0, 1.0, 1.0, 1.0).
• rotation: 4x4 rotation matrix. Determines the sphere orientation.
• lightPos: vec3 of the light position. You'll probably want to rotate this with the rotation matrix first, to make the light spin with the sphere.
• minLight: Minimum light level. Can be used to prevent fully black areas. Should be <0.2.
• mvp: ModelViewProjection matrix, usually just an orho matrix for 2D projection.

Two-sided spheres

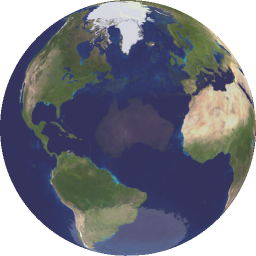
It is possible to draw a two-sided sphere. That is, the sphere is transparent and you can see the backside. To do this, just mirror the point on the sphere surface by negating the Z coordinate:

point = vec4(texCoord.xy, -z, 1.0);

Then get another texel using this new coordinate and mix the two (0.2 is a factor that controls how transparent the sphere is):

vec4 final = mix(texelA, texelB, 0.2);

You'll want to disable lighting if you do this, or find an alternative way to light the sphere.

Downloads

Included here are both the C++ and GLSL versions of the sphere code. The software version is included only for historical reasons. It is not terribly useful, but could serve as a reference point. The pixel shader version is more useful these days. You need the SDL library to compile/run the software demo. All files are heavily commented.

NOTE: The software and pixel shader versions aren't 100% equivalent! The software version does not fully support colored lights, it uses 3x3 matrices and does not anti-alias the sphere. The GLSL version supports colored lights, uses 4x4 matrices and (optionally) anti-aliases the sphere.

Sphere C++ and GLSL source code
File	sphere.zip
Size	276 KiB (282514 bytes)
Updated	Nov 16. 2012
SHA-256	f61a72fc97eada9d7480640a8955d4debb57d3f79d09f1734378f1453ba68008

Precompiled x86 Windows executable of the software renderer
File	sphere_win.zip
Size	323 KiB (330706 bytes)
Released	Jul 5. 2011
SHA-256	a249884a6eac06745fb06904df736c36611434750d74a768bea28c47a118a03e
Notes	You need the SDL library.